First Week of Class: Making Math no longer Greek to me: Greek Math, Hypatia, Pythagoras Triangles & Pie

The first day of class was interesting.  Although Math is intimidating, the historical biography and conceptual context kept my interest. Learning a mix of history along with the theoretical importance of women mathematicians will hopefully make Math seem less like “Greek to me.”

http://www.mathsisgoodforyou.com/images/people/hypatia.jpg

The first woman mathematician we were introduced to was Hypatia (370-415 A.D.).  Professor Gottlieb gave us a historical biography of Hypatia. She lived in Alexandria, Egypt and followed Greek cultural and intellectual traditions.  She was the last mathematician of the Greek world.  Her father was a mathematician.  Alexandria became the center of Greek civilization where the first University was founded.  Philosophy and Math were intertwined along with Astronomy. Hypatia was a talented lecturer, wrote several books, was said to be beautiful and strong. 

Although many have heard of Christian martyrs, Hypatia was a pagan martyr who was killed by a Christian mob that was threatened by her leadership, and her popularity in a pagan-based society.  (Although the early Christians were anti-imperialists rallying against the more powerful Pagan rulers. I wonder if Hypatia was killed by Christians after the Romans took Christianity as the official religion. Although my tendency is to root for the underdog, the Christians and Pagans flip flopped who were the status quo verses the rebels.) 

Mathematics fell into a slump and mathematical evolution went into slumber with the fall of Greek civilization.  The Romans had a clumsy numeric system and although the Greeks had advanced mathematical concepts they lacked the number zero and were mostly visual. Their mathematic concepts were mostly focused on these visual concepts.

http://www.mathsisgoodforyou.com/people/pythagoras.htm

Pythagorus was another Greek mathematician. He was born on the island of Samos and lived between c.560 and c.480 B.C.  Pythagoras made contributions to philosophy and his worship of mathematics inspired the formation of a cult by his followers.

He is most well known today for the Pythagorean theorum, a² + b² = c² in which a and b are the sides of the right angle of a triangle and c is the hypotenuse (the side opposite the right angle).  This theorum only works using right triangles. There are over 75 proofs of this theory.  Below is my explanation of Proof 3 as referenced on http://www.cut-the-knot.org/pythagoras/index.shtml:

 

 To prove Pythagorus’ theory, we can draw from the geometry we already know.
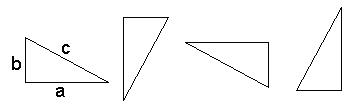To find the area of a triangle, we multiply the length (a) times the height (b) and divide by 2 [ab/2].

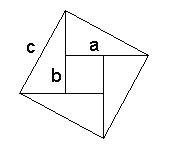
We can put 4 identical triangles together to make a square with each side having the length of c.

Once assembled, the area of the big square is found by adding the area of the 4 triangles plus the small inside square they formed.

The area of the 4 triangles is 4 times ab/2 or [4ab/2 which is the same as 2ab].

To find the area of the small square, the hole formed by the triangles, we need to know the length of its side. If we look at the upper right triangle, we can see that the long side (a) minus the short side (b) will give us the length of the inner square. So the area of the inner square is (a-b)^2.

To find the area of a square, we square the side. So, the area of the big square is c^2.

Therefore, c^2 = (a-b)^2 + 2ab.

Archealogists use the Pythagorean theorum is many ways. For example, if an archeologist finds a shard of pottery, she can use the Pythagorean theorum to determine the opening of the jar – its circumference. By drawing a line between 2 points on the curve of the shard, you have drawn a chord. By drawing 2 more lines, 1 from the radius to the curve, the other from the radius to the midpoint of the chord, a triangle is formed, so the Pythagorean theorum can be applied. Once the radius is determined, the formula for circumference 2piR can be applied. Archealogists also use the Pythagorean theorum when they plot a grid before digging up a site. (examples from the book She Does Math!)

We also discussed pi and the limits of measurements, how small inaccurances are amplified according to scale, how pi is more a conceptual tool rather than an exact mathematical recipe.

http://web.mac.com/ihor12/home/PI_DAY/

Many people celebrate Pi Day on….you guessed it….3/14!